Featured
Conventional wisdom vs data: the seventh game and the importance of serving first
Is it true that whoever wins the seventh game at 3-3 ends up winning the set? And that he who will serve first in a decider has an edge? Let’s take a look at the last ten years of Grand Slam matches’ data to see if there’s some validity to these truisms.
Published
3 years agoon
By
Staff
It is a commonly held opinion that tennis is one of the sports in which the psychological component weighs the most during matches. Proof of that is, for example, that Timothy Gallwey, one of the fathers of Business and Life Coaching, was inspired by his experience as a tennis coach in writing his best seller “The inner game of tennis”, published in 1974 and in some ways still very relevant today. In more recent times, even Agassi and Panatta have insisted a lot on this aspect in their autobiographies, with the italian using this concept in the title of his book, stating boldly that “tennis was invented by the devil”.
This close connection between what happens on the court and what happens in the mind of the players often leads to proverbial statements that, it can be said, are viewed as conventional wisdom. For example, it is believed that, precisely for psychological reasons, the seventh game, in a set tied at 3-3, is particularly important because it breaks the balance just when the set enters its bottom half. Or, again, it is commonly believed that, particularly in a match that goes to the fifth set, the first player serving has an advantage in the decisive set, thus causing in the opponent the unpleasant feeling of chasing at a time when the match is about to end.
The growing availability of structured data related to ATP matches allows us to put these claims to the test, and to verify their veracity. For this purpose, we will consider all of the men’s singles matches in Grand Slam tournaments of the last decade, from 2011 to 2021. Considering this huge database, let’s start by asking ourselves the first question: does the one player who wins the seventh game on a 3-3 tied set win the set in the end?
THE 7TH GAME
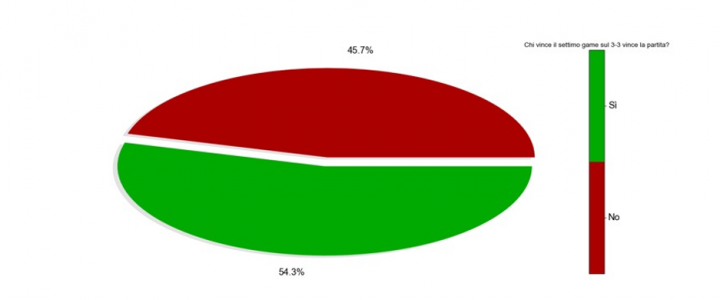
At a first glance, it would be tempting to answer in the affirmative. In fact, in 54.3% of cases whoever goes 4-3 by winning the seventh game ends up winning the set. But to attest to the validity of this first superficial observation it might seems appropriate to ask ourselves, more specifically, whether gaining the advantage at that particular moment is more significant or helpful than doing it slightly earlier, or slightly later. In other words: does winning the seventh game at 3-3 carry more weight than winning the ninth game at 4-4, or the fifth game at 2-2?
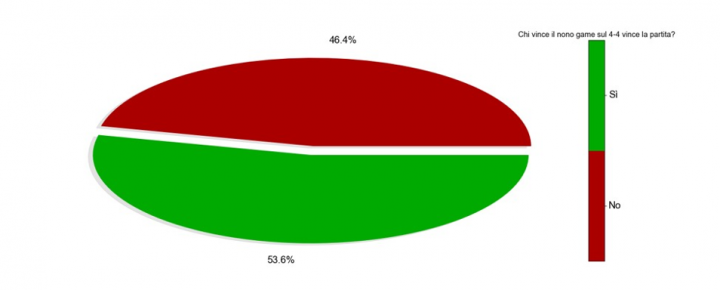
Figure 2. Percentage of cases in which whoever wins the ninth game at 4-4 wins the set, 2011-2021 Grand Slam tournaments
The set is won by whoever wins the ninth game after a 4-all in 53.6% of cases. Comparable, but slightly lower than the 54.3% recorded for the seventh-game-case in a tied set. Considering that the ninth game is closer to the ending of the set, winning a game in that situation should have a bigger impact. Therefore it would be tempting to identify a correlation, albeit not particularly strong, between the vin in the seventh game at 3-3 and winning the set. Before getting to any conclusion, however, let’s repeat the analysis, this time examining the fifth game at 2-2.
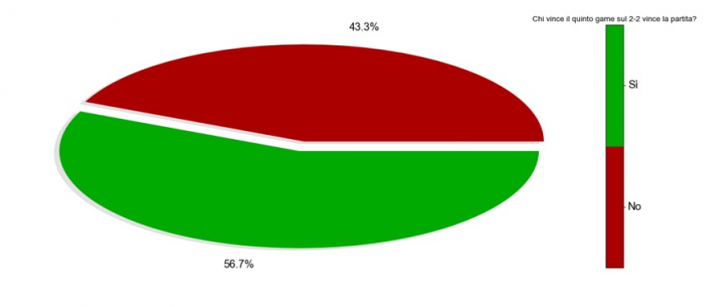
Perhaps a little surprisingly, we find that, at 2-2, the set is won in 56.7% of cases by whoever wins the fifth game. Although this game takes place further away from the end of the set, it seems to have a greater effect on the final outcome of the set. Although this fact alone is not proof in debunking the myth of the seventh game, this simple analysis has perhaps the merit of generating some doubts and some more curiosity, bringing to the forefront a hypothesis that comes from experience in more direct touch with the data. Let’s try to apply this logic to another statement as well: it’s better to serve first in the final set.
SERVING FIRST IN THE DECIDER
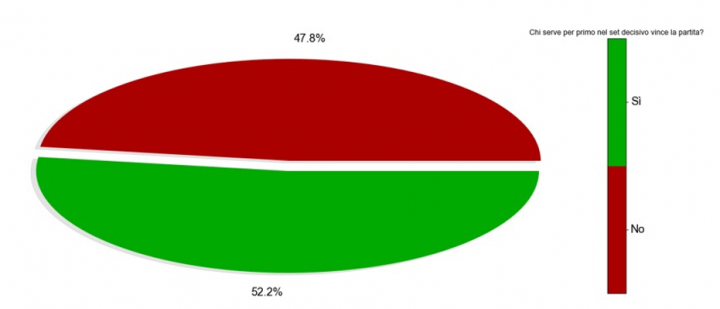
Let’s focus on the 728 Grand Slam matches that have reached the fifth set over the last ten years. Indeed, the percentage of cases in which whoever served first in these 728 occasions won the set (and, consequently, the match) is greater than 50%: to be precise, the count is 380 cases (52.2% of the total). Looking back, we can consider that, if such an advantage really exists, it is reasonable to expect it to be greater in the case of the Australian Open, Roland Garros and Wimbledon, which, for a large part of the period considered, did not provide have final set tie-breaks or super tie-breaks, with (possible) prolongation of the psychological pressure on whoever is serving second.

Australian Open, Roland Garros and Wimbledon 2011-2021
Indeed, 310 of the 576 matches of the Australian Open, Roland Garros and Wimbledon of the last 10 years in the fifth set were won by the player who served first: 53.8% of the total. A higher percentage, therefore, than the one observed also considering the US Open’ s data. We can therefore say that, in this case, at least for this analysis’ sake, there seems to be a correspondence between conventional wisdom and actual data.
Let’s now move on to the critical analysis of a third consideration, common indeed, but not necessarily supported by the data: in a hard-fought match, whoever wins the most games who go to deuce will win the match in the end.
DEUCE GAMES
To analyse this statement, and to measure its coherence with the trend of men’s singles matches in Grand Slam tournaments over the last ten years, let’s first focus on the matches with at least ten games that went to 40-40. This will allow us to focus on the statistically more significant data. Winning ten deuce games out of ten (100% of them), for example, has a different weight than winning the only one who went the distance.
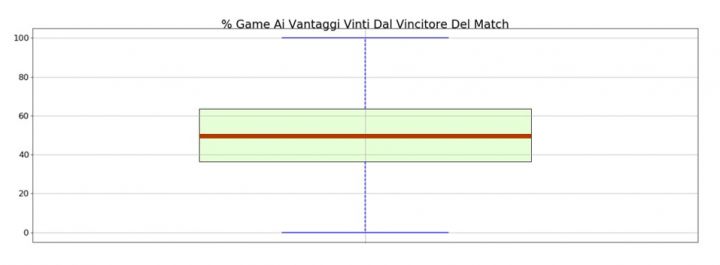
Preparing the dataset for analysis, we can see that in the last ten years 2,050 men’s singles matches have been characterized by at least ten hard-fought games. To evaluate whether, starting from this subset of games, the victory of the games with advantage points is significantly linked to match wins, let’s try to use a different graphic representation: the box-plot.
The box plot represents the statistical distribution of a variable, in this case the percentage of deuce games won by the winner of the match for the 2,050 matches considered. A commonly used concept, in the analysis of statistical distributions, is that of the percentile. Let’s imagine we order the hard-fought-game percentages won by the winners of the 2,050 matches considered in ascending order. Match number 205 of this ordered list would be classified as the to the 10th percentile of the distribution (given that 205/2050 = 0.1 = 10%). In the box plot, we see a thin yellow bar to identify the fiftieth percentile, also called the median of the distribution. If the percentage of deuce games won was particularly significant, we would expect a median value, for the winners of the matches, greater than 50% – but this is not the case.
Not just that: the green colored area of the box-plot defines the range within which the “central” 50% of the distribution is found. That is, the lower end of the green colored area coincides with the twenty-fifth percentile of the distribution, the upper end with the seventy-fifth. We observe that the central band of the distribution has the same excursion towards the lower extreme (50% -36.4% = 13.6%) than the upper one (63.6% -50% = 13.6%).
As a further check, let’s ask the data the same question once again, using a different survey tool: the ROC curve.
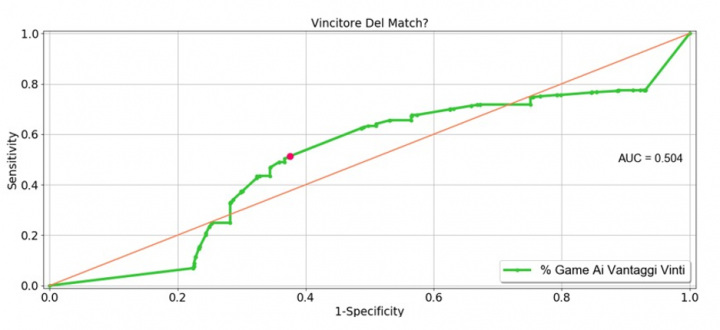
We will ask ourselves, this time, if there are thresholds (not necessarily 50%) of 40-40 games that can become decisive for the match win. Once again, for the reasons already mentioned, we will focus on matches with at least ten hard-fought games. To conduct this type of analysis, we can use the ROC curve.
To trace it, we will proceed as follows:
- every possible threshold value is considered in terms of percentage of deuce games won, starting from 0% up to 100%
- for each of these values (let’s take 10% for example) we ask ourselves: how accurate would it be to say that whoever wins more than 10% of the game at the advantages wins the match?
- the answer to this question is analysed using two components: sensitivity (i.e. the percentage of correctly identified victories) and specificity (i.e. the percentage of correctly identified losses)
- each threshold can therefore be represented as a point, drawn in a chart in which the vertical axis is represented by the wording “Sensitivity” and the horizontal axis represented by “Specificity”
- by connecting these points, a curve can be drawn, called ROC curve (Receiver Operating Curve)
- it can be shown that the area included under this curve, called AUC (Area Under the Curve) equals to the probability that, given a pair of matches (match 1 and match 2), the percentage of deuce games won by the winner of match 1 is greater than the percentage of deuce games won by the loser of match 2.
The more the AUC approaches to the value of 1, the more the element considered (in this case the percentage of deuce games won) is relevant compared to the target (the match win). We observe that, in this case, the AUC is equal to 0.504, just above 50%. The lack of relevance of deuce games supremacy therefore seems to be confirmed.
Let’s now try to ask ourselves if, indeed, as is often supposed, the victory of the first set is often decisive, especially for the underdog player.
THE FIRST SET IS KEY, ESPECIALLY FOR THE WEAKER PLAYER
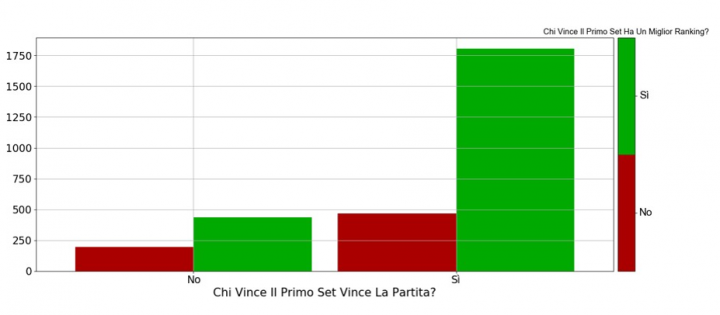
The matches in which the winner of the first set has a better ATP ranking at the end of the season is represented by the green bars of the histogram, the other matches are represented by the red bars. So let’s ask ourselves if, especially in a Grand Slam tournament, considering the men’s singles matches only and therefore a three out of five set match, the victory in the first set is relevant and, more specifically, let’s try to understand if this consideration is more valid for players who face an opponent of greater clout, or with a better ATP ranking.
First of all, we observe that 2,271 of the 2,902 matches considered ended with the victory of the player who won the first set: in other words, in 78.2% of cases whoever won the first set also won the match. This is by far the strongest pattern explored in this article. For example, if we consider the effect of ranking on the outcome of the match, we observe that in 2,238 cases out of 2,902 (i.e. in 77.1% of cases) the match is won by that player who, at the end of the season, will occupy a better position in the ATP ranking. In other words, the victory of the first set seems to “weigh” even more (albeit slightly) than the ranking in the outcome of the match.
And, as conventional wisdom teaches, the combination of the two factors is even more predictive of the name of the match winner. In fact, if the first set is won by the lower ranked player, the opponent will manage to get away with it in 30% of cases (196 matches out of 664). If, on the other hand, the better-ranked player takes the first set, then his opponent seems to have less than a 20% chance of reversing the situation (435 cases out of 2238).
This is what the data tell us, which, as always, we try to approach with a critical eye. That is, always keeping in mind Henri Poincarè, according to whom “science is made of data as a house is made of stones. But a mass of data is no more science than a pile of stones is a real house.”
Article by Damiano Verda; translated by Michele Brusadelli; edited by Tommaso Villa
Featured
EXCLUSIVE: The Grand Slam Champion Who Didn’t Get A Trophy Until 37 Years After He Died
Published
8 months agoon
14/12/2023
This year’s French Open was headlined by Iga Swiatek and Novak Djokovic triumphing in the singles tournaments but at the same time, another trophy presentation took place.
Attended by only a handful of people which included Henri Leconte and Hungarian Olympic swimming champion Daniel Gyurta, the event was conducted in honor of József Asboth. A Hungarian tennis player who in 1947 became the first Eastern European player to win a Grand Slam title at the French Open. Asboth also reached the semi-finals of Wimbledon in 1948 which is remarkably still the best-ever performance by a Hungarian man at the event.
Sadly, he never received a trophy for his French Open triumph as the tournament didn’t start that tradition until 1981. However, this year the FFT made a silver plaque in his honour with the words ‘in memory of Jozsef Asboth, Vainqueur Simple Homme, Internationaux de France 1947.‘ The gesture occurred almost 40 years after he died in 1986.
Accepting the award was Andras Ruszanov on behalf of the Asboth family. He acts as an ambassador for the tennis star and his sporting legacy. Speaking to Ubitennis, Ruszanov sheds light on Asboth’s story which he described as being marred by history, politics and bad luck. As a player, he was only allowed to leave Hungary on the condition he didn’t defect to another country. One extraordinary example was when King Gustav V of Sweden helped persuade the Hungarian regime to let him play at Wimbledon in one year.
During the late 1940s and early 1950s, Asboth was restricted from travelling to Western countries and was also prohibited from going into business with Fred Perry who offered him a job. Instead, he was instructed to coach in the Soviet Union until the fall of his regime in 1956. Eventually, he went to Belgium to with work with the national tennis federation before going to Munich, Germany. He refused to return home until Soviet troops left his country which unfortunately didn’t happen until after he passed away at the age of 69.
Here is the story of Hungary’s first and only Grand Slam champion in men’s tennis.
UBITENNIS: How did the trophy ceremony in Paris come about this year? Was it triggered by a campaign?
RUSZANOV: I have been representing the Asbóth family for about 10 years. From the very first moment, I was always guided by the goal of preserving for posterity the memory of Hungary’s first and so far only male singles Grand Slam champion. This could be the name of a tournament, street, stadium, award or even a website named after the legendary champion, such as asbothjozsef.hu, which we created in tribute to him with photos from the family archive.
On the occasion of the 100th anniversary of the birth of József Asbóth (1917- 2017), Monika Seles presented the commemorative plaque of the Hungarian Tennis Federation and Hungarian Sports Journalist Association.
In 1947, the French Open winner received no recognition other than a congratulatory handshake. From 1981 the Musketeers’ Cup was awarded to the champions after the suggestion of the late Philippe Chatrier, the president of the French and International Tennis Federation. In 2017, the idea arose that some symbolic version of the Musketeers’ Cup could serve as an eternal memory for both the Asbóth family and the Hungarian sports society to nurture and preserve József Asbóth and his sports legacy.
Both the former and current leadership of the Hungarian Tennis Federation felt the weight and importance of this mission, and the request was heard by the leadership of the French Tennis Federation – led by President Gilles Moretton. Thus, at this year’s Roland Garros, during a private ceremony in the president’s box, in the presence of President Moretton and some French legendary players such as Henri Leconte, Patrick Proisy, and the showman Mansour Bahrami, I was able to receive the award on behalf of the Asbóth family from the two-time Grand Slam champion, Hall of Famer Amélie Mauresmo, who serves as the tournament director of French Open. The Hungarian sports diplomacy was represented by the Olympic champion Dániel Gyurta on behalf of the Hungarian Minister of Foreign Affairs, and the sports media was represented by György Szöllősi, vice president of AIPS Europe (European Sports Journalists Association).
This current recognition was the ‘fruit’ of several years of work, and the silver plaque that has just been handed over has the Musketeer’s Cup for the men’s singles champion in engraved form.

UBITENNIS: Was it true that Jozsef was only allowed to leave Hungary on a guarantee he would not defect to another country?
Yes, Asbóth’s entire career was cut in two by history, politics and bad luck. He played in a total of 10 Grand Slams, but 8 years passed between his 2nd and 3rd major. In his heyday – between the ages of 22 and 30 – he could not participate in a single Grand Slam, because of World War II and its consequences. Then he managed to win the 4th Grand Slam tournament of his life at the age of almost 30. Then the ordeals came again…
In 1948, Asbóth was seeded number 2 in Paris (which is still a record for a Hungarian male player) in the main draw. However, he could not defend his title, as his mother passed away the day before the start of the tournament, so Asbóth withdrew and flew home to Hungary.
His appearance at the next Slam, in Wimbledon, was also in jeopardy, as the communist leadership in his country did not look favourably on his performances in foreign tournaments. One of his great admirers, King Gustav V of Sweden had to give a personal guarantee to the Hungarian communist government that Asbóth would return to his country and not emigrate abroad. Thanks to the intervention of Sweden’s longest-reigning monarch, the Hungarian top player was able to attend Wimbledon and so far achieved the greatest success of a Hungarian male tennis player.
He reached the semi-final for the first time in Wimbledon and according to the unanimous opinion of the experts, Asbóth played the most spectacular tennis of all the players. He even captivated the legendary Harry Hopman, who patted Asbóth on the shoulder and said: “Listen here, mate, grass is your element”. Unfortunately, in the quarter-final match, Asbóth’s ankle was injured in such a way that the next day it was so swollen that he could barely walk, nonetheless, he played with all the more heart and energy (he lost the 2nd set 14-12!).
A healthy Asbóth would have had a real chance not only to reach the final but even to win the title. After his loss in the semi, despite the painful defeat and injury, he praised his opponent and did not make excuses!
Then the Communist Party leadership did not allow him to travel to Paris until 1954, and never to Australia or the States.
UBITENNIS: During the time of his playing career Hungary was going through oppression from the soviet union communist regime. How did he manage to cope with this?
RUSZANOV: Politics had an impact on his entire career, this is especially true for the years following World War II, to the beginning of communist rule, where they governed according to Stalinist practice. The economy was nationalized, and the communist rule serving the interests of the Soviet empire began in political life.
Asbóth and some of his fellow tennis players also took part in the post-war debris clean-up, and from the 1948s onwards, his travels to the West were restricted by the communist dictatorship. Instead of foreign tournaments, he was sent to Moscow to train and instruct Soviet coaches. But it also happened that the president of neighbouring Romania had to stand as the doubles partner of Petru Groza on the tennis court of the president’s private mansion, on a party order. And it happened that the president’s bodyguard was sitting in the chair umpire’s seat with a rifle in his hand.
Fred Perry, with whom he maintained an excellent friendship and whose clothing bearing his name appeared in 1952, offered Asbóth to join his company, but the Hungarian Communist Party did not agree to this.
After the defeat of the 1956 revolution, Asbóth retired from active play and accepted the invitation of the Belgian federation, or better said he could have accepted, since this also had to be approved by the party leadership. In Belgium, he became the head of the youth development program, and later he was asked to become head coach by the Iphitos tennis club in Munich.
He made a promise that he would not return to his country as long as Soviet troops were stationed in Hungary. Unfortunately, he could not live to see them leave, as he died on September 11, 1986, in Germany.
Embed from Getty ImagesUBITENNIS: How is his legacy viewed back home? Do many Hungarian players nowadays speak about him?
RUSZANOV: In Hungary, soccer is considered a national sport, and the legendary Ferenc Puskás, the captain of the national team known as the ‘Golden Magyar’ (unbeaten for 4 years in the 50s and beat England in the match of the century in 1953), is the best-known Hungarian athlete in the world and the FIFA Goal of the Year award also bears his name. The other fact is that in Hungary, the Olympic and World Championships are incredibly respected, so the names of the Olympic and World Champion athletes are almost always classified in the category of Hall of Fame in the country.
Unfortunately, József Asbóth was successful in an era when tennis did not enjoy such support, even though from the end of the 1940s the matches were played in front of a sold-out crowd. Largely thanks to József Asbóth, and Zsuzsa Körmöczy (1958 Roland Garros champion).
At the beginning of the 21st century, Asbóth’s successes have faded a bit, but on the one hand, with the appearance of the new Hungarian tennis generation, his name is being heard more and more. As the manager of the Asbóth sports legacy, I will do everything in my power to make his name known to as many Hungarians as possible.
Asbóth’s name inevitably always comes up, even in connection with Roland Garros or Wimbledon, because to this day he achieved the greatest individual success in Hungarian men’s tennis at these two Grand Slam events! I hope that this current recognition will also promote the renaissance of the Asbóth cult!
UBITENNIS: Are there any other stories of interest about him that you can share?
RUSZANOV: On July 6, 1938, in Budapest, after winning Wimbledon, Don Budge, who was on the European tour, and the then unknown 20-year-old Hungarian talent, József Asbóth, faced each other in an exhibition match. Asbóth played brilliantly and so well that American world number one gave up the match in the 3rd set with Asbóth’s lead, claiming that he had to catch the train to Prague. (At that time, Budge already won his 5th Grand Slam in a row, and a few weeks later he also triumphed at the US Open.)
József Asbóth has also a 1-0 H2H record against Roy Emerson, the male tennis player who has won the most Grand Slam titles of all time (16 singles and 12 doubles). Emerson played for the first time at Roland Garros at the age of 17, and in the first round, he faced the then almost 37-year-old Asbóth. Being a rookie from Australia, he did not know the former champion, ran into the dressing room and asked Ken Rosewall what he knew about Asbóth. Rosewall just said “I’m sorry” and held out his right hand and said “five fingers, that’s about how many games you’re going to win in three sets.”
When Emerson went out on the court before the match, he met an elegant gentleman in long pants. He thought he was the referee, so he introduced himself to him, to which he replied, “I’m József Asbóth”. During the warm-up, Asbóth did not foul a single ball and he played with so much feeling that his strokes almost spoke. Emerson sensed that he was in great trouble. The match began, and Asbóth toyed with the Australian as he wanted. He drove it from one side to the other, Emerson ran around like a chased wild animal. He was covered in sweat and grimy from head to toe, and Asbóth’s long pants didn’t even show a crease. Rosewall laughed himself to death in the stands. Emerson was in good shape, but after two sets he started to get very tired after Asbóth constantly controlled the game.
After the lost match Emerson asked who the hell is this guy? And Rosewall said, “Well, go out and look at the list of champions on the wall of the stadium”. Seeing that Asbóth won in 1947, Emerson didn’t feel so bad anymore.
UBITENNIS: Finally, what other tennis achievements did he produce outside of the Grand Slams?
RUSZANOV: Between April 1 and September 16, 1940, Asbóth participated in 11 tournaments, of which he won 9 (Genoa, Taormina, Palermo, Budapest, Wiesbaden, Gödöllő, Budapest, Milan and Merano).
In 1947, Asbóh participated in 12 tournaments, 3 domestic and 9 international best tournaments, of which he played in the final 8 times, of which he won 5 times (San Remo, Nice, Paris and twice in Budapest).
In 1948, he started in 11 competitions, and we find his name in 7 finals, of which he won the trophy 5 times. After Beaulieu, Cannes and Nice, he did not find a winner in Monte-Carlo (the predecessor of today’s Monte-Carlo Masters).
He won 24 matches in the Davis Cup and in 1949 he was able to play in the semifinals with the Hungarian team.
Among Asbóth’s mentors, we also find a name who is a defining figure in the history of tennis, one of the (perhaps the best) musketeers, the legendary Henri Cochet. The Hungarian player’s entire career was influenced by the French champion, which is why, like Cochet, he always wore a short-sleeved white shirt and long white pants throughout his career.

At this same time of the year in 2022, Carlos Alcaraz announced to the tennis community that he was ready to propel himself into the forefront of the sport. He reached the semifinals of the BNP Paribas Open at Indian Wells before losing to countryman Rafael Nadal amidst almost impossibly windy conditions in the California dessert. Although Alcaraz had already reached the quarterfinals of the 2021 U.S. Open, the stellar Indian Wells showing last year propelled him to another level.
In short order, Alcaraz won his first Masters 1000 title in Miami, captured another of those elite crowns in Madrid, and, at the end of last summer, took the U.S. Open title in New York. With that breakthrough triumph at a major, Alcaraz went to No. 1 in the world, and he concluded the season still stationed at the very top of tennis. He has been hobbled by injuries too often since last November and consequentially missed the Australian Open, but now this 19-year-old sensation is back on top of the world at No. 1 following a 6-3, 6-2 final round victory over Daniil Medvedev in the final at Indian Wells.
That was no mean feat for this strikingly mature champion. He is the youngest man ever to secure both the Miami and Indian Wells titles. Not since Roger Federer in 2017 had a male player taken this prestigious crown without losing a set. Medvedev was enjoying the second longest winning streak of his career of 19 match victories in a row. He was striving for a fourth consecutive ATP Tour title in a debilitating five-week span. He had seemingly almost forgotten how to lose after finding his form in Rotterdam in mid-February. He won there by toppling Jannik Sinner in the final. On he went to Doha, where he stopped Andy Murray in the final. The following week in Dubai, Medvedev ended a four match losing streak against Novak Djokovic with a 6-4, 6-4 semifinal win and then obliterated countryman Andrey Rublev 6-2, 6-2 in the title round.
Medvedev’s form fluctuated at Indian Wells but he seemed to be progressing as he headed into the final. But he had faced Alcaraz only once before. That was in 2021 at Wimbledon and Medvedev came through easily when Alcaraz was not the same player. So this collision at Indian Wells in the final was going to be revealing one way or another for two great players who figure to meet many more times on big occasions in the years ahead.
Some authorities believed Medvedev would exploit his experience, maintain his winning streak, and add another title to his collection. Of the 18 tournaments Medvedev has amassed starting in 2018, all but one have been on hard courts. But seldom has he been beaten as soundly as was by Alcaraz at Indian Wells. The Spaniard put 76% of his first serves in play compared to 65% for Medvedev. Alcaraz won 81% of his first serves points while Medvedev finished 20% behind his opponent in that department. Meanwhile, Alcaraz secured 58% of his second serve points and Medvedev finished well below that mark at 41%. Not once did Medvedev even reach break point. That is a rarity.
The humiliation for Medvedev transcended those facts. Time and again, Alcaraz set the tactical agenda. He caught Medvedev off guard with selective serve-and-volley combinations. He used the drop shot magnificently. He went for his shots freely and stayed away from the rhythmic long rallies on which Medvedev feasts. He kept Medvedev guessing for 70 painful minutes. For his part, Medvedev inexplicably attempted to match or surpass the Spaniard’s backcourt pace. He pressed off both sides. His forehand was well below par. And when Medvedev had the chance to prolong rallies and play more on his own terms, he impatiently went for bigger shots which backfired almost completely. His mind was muddled. Essentially and surprisingly, Medvedev was not ready to fight with his usual ferocity. He collapsed against an unrelenting Alcaraz.

Alcaraz was primed from the outset. He raced to 3-0 in the opening set, sweeping 12 of 15 points on the process. Medvedev professionally started imposing himself and held serve three times after falling behind. In his last two service games he conceded only one point as he located his delivery more accurately. But Alcaraz was unswerving on his own delivery, winning 20 of 26 points in five service games. Serving for the set at 5-3, he held comfortably at 15, closing out that game by serve-volleying on the last two points.
Medvedev had seemingly found his bearings after a slow start, but Alcaraz pounced in the opening game of the second set and broke his dispirited opponent at love. Medvedev gave that game away with two unforced errors off the ground, an errant backhand volley and a double fault. Alcaraz swiftly held at love and moved ahead 0-30 on Medvedev’s serve in the third game. He had won ten points in a row.
Alcaraz went on to break Medvedev again for 3-0 and surged to 4-0 with another routine hold. It had taken him only 17 minutes to build that second set lead. The rest was a formality. Alcaraz closed out the account without stress despite being taken to deuce when he served for the match at 5-2.
That it all came down to a duel between Alcaraz and Medvedev— the last two U.S. Open champions—for the first Masters 1000 crown of 2023 made perfect sense. As an unvaccinated player, Novak Djokovic was not permitted to enter the United States to compete at Indian Wells and Miami. Rafael Nadal—three time champion at Indian Wells and runner-up to Taylor Fritz a year ago—was not ready to return to the ATP Tour after his latest injury that led to a second round loss at the Australian Open.
With the two icons absent, the cognoscenti of tennis hoped for an enticing final round confrontation between Alcaraz and Medvedev. The match did not come even close to delivering on its considerable promise, but the fact remained that they both deserved to be there. The beguiling Spaniard took apart the Australian Thanasi Kokkinakis 6-2, 6-3 in the second round, ousted the tall Dutchman Tallon Griekspoor 7-6 (4), 6-3 in the third round, and then needed less than 47 minutes to defeat an ailing Jack Draper of Great Britain. Alcaraz led 6-2, 2-0 in that clash when the left-hander was forced to retire.
Alcaraz was rolling now. He had lost all three of his previous appointments against the charismatic Felix Auger-Aliassime, who had improbably erased six match points against him in a round of 16 win over Tommy Paul. But this time around against FAA, Alcaraz was exhilarated under the lights and he came through comfortably 6-4, 6-4. The serving statistics from this encounter are telling. Alcaraz won 81% of his first serve points, which was 11% better than the Canadian. The Spaniard took a respectable 59% of his second serve points, while Auger-Aliassime stood far below at 42%.
Alcaraz was the superior performer across the board during this quarterfinal encounter. He was sounder and cagier, quicker and sprightlier. His return was first rate across the two sets, and he backed up his own delivery with uncanny efficiency. It was a confidence building triumph in every respect, and just what he needed as he headed into the semifinals to take on Jannik Sinner.
The Italian had overcome the defending champion Fritz in a sparkling quarterfinal skirmish lasting three absorbing sets. Sinner blasted away spectacularly against the Californian and he had the upper hand in the vast majority of long rallies contested on an exceedingly windy night.
Sinner is industrious, unwavering and often enterprising. He had been victorious in two of his four showdowns with Alcaraz, prevailing in a memorable four set, round of 16 clash on the Centre Court at Wimbledon last year before losing what may well have been the best tennis match in all of 2022 at the U.S. Open. In that quarterfinal confrontation under the lights in Arthur Ashe Stadium, Sinner had a match point in the fourth set of a pendulum swinging contest before Alcaraz rallied again from a break down to take the fifth set and prevail 6-3, 6-7 (7), 6-7 (0), 7-5, 6-3 in five hours and fifteen minutes of spellbinding tennis.

No wonder so many learned observers were looking forward to the fifth career collision between two players who will surely be taking prestigious prizes away from each other for the next decade. Alcaraz moved out in front 4-2 before Sinner took eleven points in a row (and 12 of 14) on his way to a 5-4 lead. Sinner needed that first set more than Alcaraz. The Italian reached 15-30 in the tenth game but narrowly missed a return. Alcaraz held on for 5-5 but soon faced a set point in the twelfth game. Sinner was right where he wanted to be, on the edge of a first set victory.
But Alcaraz is frequently at his best when faced with the sternest of challenges. He took a short blocked return from Sinner and released one of his patented drop shots. Sinner chased it down, but his passing shot was much too high. Alcaraz moved easily to his right and punched a forehand volley winner into the open court. The set would be settled in a tie-break, and Alcaraz was too good, breaking a 4-4 deadlock by sweeping three points in a row, sealing that sequence 7-4 with a scorching flat backhand winner crosscourt. Alcaraz made one break count in the second set and succeeded 7-6 (4), 6-3. It was a remarkable performance highlighting Alcaraz’s match playing acumen.
As for Medvedev, making it to the final was a much tougher task. He handled Brandon Nakashima 6-4, 6-3 in the second round, although the match was more competitive than the score would indicate. Then he overcame Ilya Ivashka 6-2, 3-6, 6-1 to reach the round of 16 and an eagerly awaited clash with Sascha Zverev.
Zverev has had a difficult time rediscovering the heights of his game after missing the second half of 2022 following the abysmal ankle injury he suffered against Nadal in the semifinals of Roland Garros. But he had started playing better tennis in Dubai a few weeks back before losing a semifinal to Andrey Rublev. Zverev largely outplayed Medvedev at Indian Wells but, three times over the course of the match, he squandered 0-40 openings. He also missed out on 15 of 17 break point opportunities.
On top of all that, Medvedev rolled his ankle in the middle of the second set and needed the trainer. Somehow he survived despite the injury, winning 6-7 (5), 7-6 (5), 7-5 despite getting broken at 5-4 in the final set when he served for the match the first time. Zverev then played horrendously at 5-5, double faulting on break point. Medvedev escaped.

He remained concerned about the ankle in the quarterfinals against Alejandro Davidovich Fokina, and fell again, cutting his thumb in the process. Nevertheless, he got the win 7-5, 6-3. Two days off helped his cause considerably, and Medvedev looked fine physically on all fronts during his semifinal against Frances Tiafoe.
In fact, Medvedev was near the top of his game in establishing a 7-5, 5-3 lead. Seldom if ever has he produced so many breathtaking forehand passing shots, and, in turn, he was hardly missing from the baseline. But Tiafoe is doubly dangerous when he is behind, as he demonstrated so boldly last year in the U.S. Open semifinals against Alcaraz when he got up off the canvas after looking down and out to force a fifth set.
In this case, Tiafoe serve-volleyed his way out of two match points in the ninth game of the second set, and saved a third by provoking a forehand error on the stretch from Medvedev. Medvedev could not serve out the match at 5-4 but he broke right back at love in the eleventh game and served for the match a second time at 6-5. He reached 40-0 but Tiafoe erased four more match points in that astounding game. On they went to a tie-break, but an unruffled Medvedev did not fret. He took that sequence seven points to four, concluding the contest with a service winner and an ace. Medvedev was deservedly victorious 7-5, 7-6 (4). Not until he captured that match was his head cleared and his outlook altered. In the middle of the tournament, the 27-year-old was complaining vocally about the conditions, claiming that the slow conditions were not really hard court tennis as he knew it. That was a simple case of Medvedev irrationality.
A day later, Medvedev was trounced by a top of the line Alcaraz. He took the defeat graciously, recognizing that he had hit a physical and emotional wall after so much success in recent weeks. He also realized that Alcaraz had played a magnificent match. The Spaniard will be buoyed by the victory and confident that he has all the tools to confront Medvedev in the years to come. But Medvedev is a very studious fellow who will go back to the drawing board and examine what it will take to unsettle a surging Alcaraz the next time they meet.
Despite the setback, Medvedev has moved back to No. 5 in the world. It won’t be long before he finds himself in the top three, right up there with the pace setters Alcaraz and Djokovic. They are clearly the three best players in the world right now. It will be fascinating to follow their exploits. Djokovic, of course, was easily the best in the game across the second half of 2022 from Wimbledon on. He then opened his 2023 campaign by winning a tenth Australian Open and a 22nd major in the process. After his loss to Medvedev in the Dubai semifinals, the Serbian has been unable to play. That clearly contributed to Alcaraz regaining the top spot in the ATP Rankings, although the Spaniard must hold onto his crown in Miami to prevent Djokovic from taking back the No. 1 ranking.
A revitalized Djokovic will surely return at full force on the clay starting in Monte Carlo and perform purposefully as he chases a third French Open crown. Medvedev will need to prove that he can raise his clay court standards from years gone by. Alcaraz is riding high right now and will be tough to beat as he defends his crown in Miami. I expect him to realize that feat.
All signs point to some gripping battles between Djokovic and Alcaraz on the clay in Europe. If Nadal is healthy, he will be right there with them vying for the titles on the dirt. He will be determined to play his typical brand of unimaginably effective and inspiring clay court tennis. We are in for some astonishing matches in the coming weeks among these top players.
But, for a few days at least, Carlos Alcaraz should celebrate one of the best weeks of his young career at Indian Wells, and try to appreciate how well he is playing before he shifts his attention to winning again in Miami and pursing other primary targets. He owes it to himself to briefly but completely enjoy his latest triumph as much as possible. I suspect he will do just that.
ATP
United Cup Daily Preview: The United States Plays Italy in the Final
Published
2 years agoon
07/01/2023
On Sunday in Sydney, the champions of the inaugural United Cup will be decided.
In the semifinals, the United States completed a clean sweep of Poland on Saturday, while Italy defeated Greece 4-1 despite Matteo Berrettini’s loss to Stefanos Tsitsipas in an excellent three-setter. Sunday’s play will feature four singles matches and a mixed doubles contest, with the first nation to win three matches to be crowned the United Cup champions.
Each day, this preview will analyze the two most prominent matches on the schedule. Sunday’s play gets underway at 1:00pm local time.
Jessica Pegula [USA] vs. Martina Trevisan [ITA] – Starts at 1:00pm
This will be the first match of the day. Pegula has gone 3-1 at this event, losing to Petra Kvitova in her first match, but defeating World No.1 Iga Swiatek on Friday. Trevisan is 2-2, though she helped propel Italy into this final with an epic victory over Maria Sakkari on Friday.
In their first career meeting, Jessica is a significant favorite. Pegula was 42-21 last season, reaching a career-high of ranking of No.3 thanks to her consistency at big events. And the fast-playing hard courts strongly favor her game, as they helped her reverse her lopsided rivalry with Swiatek in dominating fashion. By contrast, Trevisan had a losing record on hard courts last season, claiming just six tour-level matches in main draws on this surface.
The second match of the day will feature Frances Tiafoe taking on Lorenzo Musetti. Both men are 4-0 to this stage, and this matchup feels like it could easily go either way.
Taylor Fritz [USA] vs. Matteo Berrettini [ITA] – Not Before 5:30pm
This will be the third match of the day. Both players are 3-1 thus far at this event. Fritz’s loss came to Cam Norrie in the city finals, while Berrettini’s loss came in Saturday evening’s semifinals to Stefanos Tsitsipas. Notably, Matteo spent about an hour longer on court Saturday than Taylor, with the Italian’s match ending much later in the day.
Fritz is 2-0 against Berrettini. His victories came four years ago in Davis Cup on an indoor hard court, and two years ago at Indian Wells on in outdoor hard court. Taylor should be the fresher player on Sunday, and with the decided edge in their head-to-head, the American is the favorite to prevail.
The fourth match of the day sees Madison Keys take on Lucia Bronzetti, with Keys heavily favored. And the mixed doubles at the end of the day is scheduled to feature Pegula and Fritz against Trevisan and Berrettini. Overall, the United States is the favorite to win the first-ever United Cup.
The United Cup daily schedule is here.

Paris Olympics Daily Preview: Osaka Plays Kerber, Nadal Teams with Alcaraz

Tennis At The 2024 Paris Olympics: Five Things You Need To Know

Rafael Nadal’s Double Olympic Bid In Doubt, Confirms Coach Moya

Matteo Berrettini extends his winning streak to eight consecutive matches to reach the semifinal in Kitzbuehl

Novak Djokovic’s Potential Second Round Clash With Rafael Nadal Headlines Olympics Draw

Wimbledon Says No To Euros, No To Sunday Starts But Yes To An Andy Murray Statue

Wimbledon: Frances Tiafoe – ‘I Was Losing To Clowns And Took The Game For Granted’

Andrey Rublev Explains On-Court Outburst Following Wimbledon Exit

EXCLUSIVE: Sumit Nagal Brings Indian Tennis To The Main Stage But He Has Concerns About The Future

(VIDEO) Jannik Sinner Set To Renew Rivalry With Defending Champion Alcaraz, Djokovic Ready To Play

(VIDEO) What Is Wrong With Jannik Sinner?

(VIDEO) Ubaldo And Steve Flink – “Djokovic Was Too Flat, Alcaraz Triumphs Yet Again At Wimbledon”

(VIDEO) Steve Flink, Ubaldo On The Wimbledon Women’s Final: ‘The Better Player Won But Did Inexperience Play A Part?’

(VIDEO) Ubaldo And Steve: “Paolini’s Resilience Earns Her Another Stunning Grand Slam Final”

(VIDEO) Amazing Lorenzo Musetti Sets Up Djokovic Showdown At Wimbledon
Trending
-

 Hot Topics3 days ago
Hot Topics3 days agoNo Olympic Village Stay For Novak Djokovic In Paris, Says Delegation
-

 Latest news3 days ago
Latest news3 days agoWorld No.634 Laura Samson Reaches First WTA Quarter-Final At 16
-

 Hot Topics2 days ago
Hot Topics2 days ago(VIDEO) What Is Wrong With Jannik Sinner?
-

 Hot Topics3 days ago
Hot Topics3 days agoFive Talking Points Ahead Of The 2024 Olympic Men’s Tennis Tournament
-

 Focus2 days ago
Focus2 days agoJannik Sinner Withdraws From Olympics Due To Tonsillitis
-

 Focus2 days ago
Focus2 days agoMatteo Berrettini battles past Alejandro Tabilo to reach the quarter final in Kitzbuehl
-

 Focus2 days ago
Focus2 days agoCoco Gauff ‘Proud’ Of Being Named Olympic Flagbearer alongside Lebron James
-

 Hot Topics2 days ago
Hot Topics2 days agoAndy Murray At Peace With Retirement Decision Ahead Of Olympic Farewell









